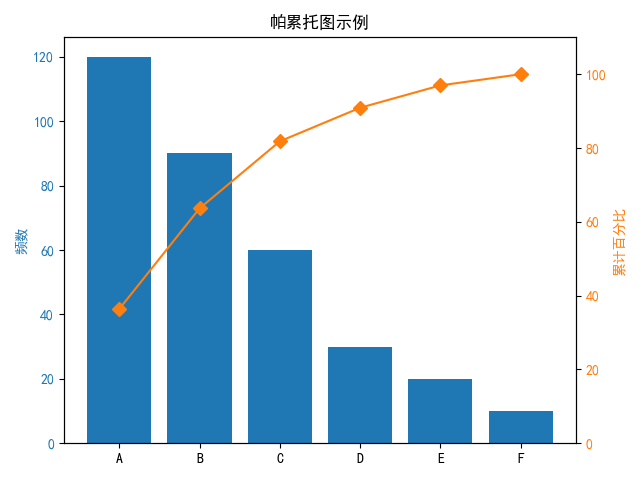
帕累托图

• 帕累托图（Pareto Chart）是一种结合了柱状图和折线图的统计图表，常用于显示各因素的频数及其累计百分比，帮助识别主要问题或关键因素。

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
plt.rcParams['font.sans-serif'] = 'SimHei'
# 示例数据：类别及对应频数
data = {
    '类别': ['A', 'B', 'C', 'D', 'E', 'F'],
    '频数': [120, 90, 60, 30, 20, 10]
}

df = pd.DataFrame(data)

# 按频数降序排序
df = df.sort_values(by='频数', ascending=False).reset_index(drop=True)

# 计算累计频数及累计百分比
df['累计频数'] = df['频数'].cumsum()
df['累计百分比'] = 100 * df['累计频数'] / df['频数'].sum()

# 创建双轴图
fig, ax1 = plt.subplots()

# 绘制柱状图 - 频数
ax1.bar(df['类别'], df['频数'], color='C0')
ax1.set_ylabel('频数', color='C0')
ax1.tick_params(axis='y', labelcolor='C0')

# 创建第二个纵轴 - 累计百分比
ax2 = ax1.twinx()
ax2.plot(df['类别'], df['累计百分比'], color='C1', marker='D', ms=7)
ax2.yaxis.set_major_formatter(plt.PercentFormatter())
ax2.set_ylabel('累计百分比', color='C1')
ax2.tick_params(axis='y', labelcolor='C1')
ax2.set_ylim(0, 110)

# 标题和布局
plt.title('帕累托图示例')
plt.tight_layout()
plt.show()

ROC曲线

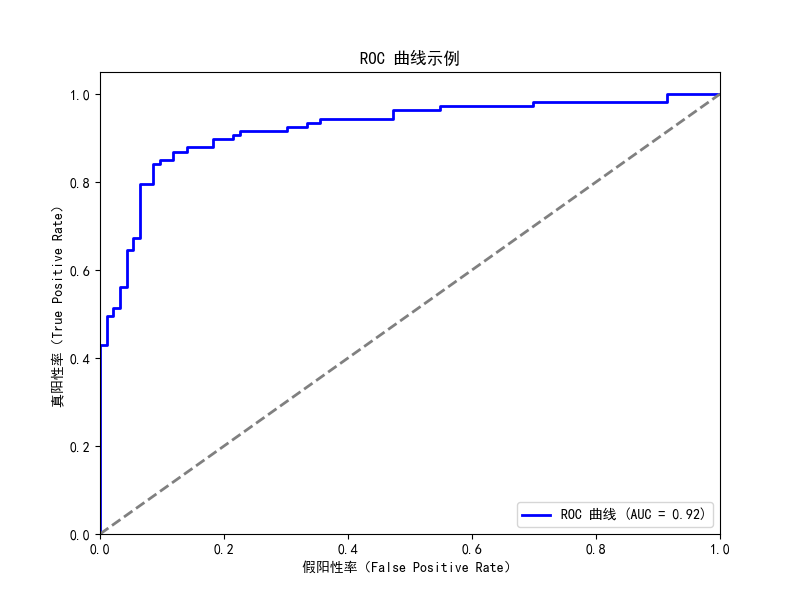
• ROC（Receiver Operating Characteristic）曲线 是用于二分类模型性能评估的重要工具，特别适合不均衡数据集。它反映了分类器在不同阈值下的假阳性率（False Positive Rate, FPR）与真阳性率（True Positive Rate, TPR）的关系。

  • 真阳性率（TPR）：也叫召回率，表示被正确识别为正类的比例。计算公式：TPR = TP / (TP + FN)
  • 假阳性率（FPR）：错误地被识别为正类的负类比例。计算公式：FPR = FP / (FP + TN)

• ROC曲线是以FPR为横轴，TPR为纵轴绘制的曲线，越接近左上角（FPR低，TPR高）说明模型越好。

• AUC（Area Under Curve） 是ROC曲线下的面积，表示模型整体的分类能力。AUC越接近1越好，0.5相当于随机猜测。

import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve, auc
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_classification
import matplotlib as mpl

# 设置中文字体
mpl.rcParams['font.sans-serif'] = ['SimHei']  # 指定字体为 SimHei（黑体）
mpl.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题

# 生成模拟二分类数据集
X, y = make_classification(n_samples=1000, n_features=20, n_classes=2, random_state=42)

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 训练逻辑回归模型
model = LogisticRegression()
model.fit(X_train, y_train)

# 预测测试集正类概率
y_score = model.predict_proba(X_test)[:, 1]

# 计算假阳性率（FPR）、真阳性率（TPR）和阈值
fpr, tpr, thresholds = roc_curve(y_test, y_score)

# 计算 AUC 值
roc_auc = auc(fpr, tpr)

# 绘制 ROC 曲线
plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, color='blue', lw=2, label=f'ROC 曲线 (AUC = {roc_auc:.2f})')
plt.plot([0, 1], [0, 1], color='gray', linestyle='--', lw=2)  # 随机猜测参考线
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('假阳性率（False Positive Rate）')
plt.ylabel('真阳性率（True Positive Rate）')
plt.title('ROC 曲线示例')
plt.legend(loc="lower right")
plt.show()

数据挖掘算法

回归

特点

• 目标：预测连续值
• 模型：连续函数 $f(X) \rightarrow Y$
• 常用指标：MAE、MSE、MedAE、R2R^2、EVS

线性回归 (Linear Regression)

from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error, mean_squared_error, \
                            median_absolute_error, explained_variance_score, r2_score
import pandas as pd

# 1⃣ 读取数据
# 读取数据文件 'financial.csv'，数据集包含自变量 X 和因变量 y
data = pd.read_csv("financial.csv")
X = data.drop(columns="target")   # 自变量 X，去掉目标列 'target'
y = data["target"]               # 因变量 y，目标列

# 2⃣ 划分数据集
# 将数据集按 80/20 的比例划分为训练集和测试集，随机种子为 125
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.20, random_state=125)

# 3⃣ 建模与训练
# 使用线性回归模型并对训练数据进行训练
model = LinearRegression().fit(X_train, y_train)

# 4⃣ 预测
# 使用训练好的模型对测试数据进行预测
y_pred = model.predict(X_test)

# 5⃣ 评估
# 输出各种回归评估指标
print("MAE :", mean_absolute_error(y_test, y_pred))         # 平均绝对误差
print("MSE :", mean_squared_error(y_test, y_pred))         # 均方误差
print("MedAE :", median_absolute_error(y_test, y_pred))    # 中位绝对误差
print("EVS :", explained_variance_score(y_test, y_pred))   # 解释方差得分
print("R² :", r2_score(y_test, y_pred))                    # R² 决定系数

逻辑回归（含ROC曲线绘制）

虽名为“回归”，也可以进行二元或多元分类。

from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, precision_score, recall_score, \
                            confusion_matrix, roc_curve, auc
import pandas as pd
import matplotlib.pyplot as plt

# 读取数据
data = pd.read_csv("financial.csv")
X = data.drop(columns="label")  # 自变量 X
y = data["label"]              # 因变量 y

# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.20, random_state=125)

# 初始化逻辑回归模型并训练
clf = LogisticRegression(max_iter=1000).fit(X_train, y_train)
y_pred = clf.predict(X_test)  # 对测试集进行预测

# 输出分类指标
print("Accuracy :", accuracy_score(y_test, y_pred))        # 准确率
print("Precision:", precision_score(y_test, y_pred))       # 精确度
print("Recall   :", recall_score(y_test, y_pred))          # 召回率
print("ConfMat  :\n", confusion_matrix(y_test, y_pred))    # 混淆矩阵

# === ROC 曲线 ===
# 计算预测结果的概率并绘制 ROC 曲线
y_score = clf.predict_proba(X_test)[:, 1]  # 获取正类的概率
fpr, tpr, _ = roc_curve(y_test, y_score)   # 计算假阳性率与真阳性率
roc_auc = auc(fpr, tpr)                    # 计算 AUC 值

# 绘制 ROC 曲线
plt.figure()
plt.plot(fpr, tpr, lw=2, label=f"ROC (AUC={roc_auc:.2f})")
plt.plot([0, 1], [0, 1], "--")             # 参考线：完全随机
plt.xlabel("False Positive Rate")
plt.ylabel("True Positive Rate")
plt.title("ROC Curve — Logistic Regression")
plt.legend()
plt.show()

分类

特点

• 输出：离散类别
• 输入：样本属性
• 训练方式：监督学习
• 常用指标：Accuracy、Precision、Recall、F1、ROC/AUC

决策树 (Decision Tree)

from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, precision_score, recall_score, confusion_matrix
import pandas as pd

# 读取数据
data = pd.read_excel("sales_data.xls")
X = data.drop(columns="label")  # 特征自变量
y = data["label"]              # 目标标签

# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.20, random_state=125)

# 创建决策树分类器并训练
dtc = DecisionTreeClassifier(criterion="entropy").fit(X_train, y_train)
y_pred = dtc.predict(X_test)  # 对测试集进行预测

# 输出分类指标
print("Accuracy :", accuracy_score(y_test, y_pred))        # 准确率
print("Precision:", precision_score(y_test, y_pred))       # 精确度
print("Recall   :", recall_score(y_test, y_pred))          # 召回率

K 近邻 (K‑NN)

from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.datasets import load_iris

# 加载 Iris 数据集
iris = load_iris()
X_train, X_test, y_train, y_test = train_test_split(
    iris.data, iris.target, test_size=0.20, random_state=125)

# 创建 K-近邻分类器并训练
knn = KNeighborsClassifier(n_neighbors=5).fit(X_train, y_train)
y_pred = knn.predict(X_test)  # 对测试集进行预测

# 输出准确率
print("Accuracy :", accuracy_score(y_test, y_pred))  # 准确率

支持向量机 (SVM)

from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.datasets import load_digits

# 加载手写数字数据集
digits = load_digits()
X_train, X_test, y_train, y_test = train_test_split(
    digits.data, digits.target, test_size=0.20, random_state=125)

# 创建支持向量机分类器并训练
svc = SVC().fit(X_train, y_train)
# 输出准确率
print("Accuracy :", accuracy_score(y_test, svc.predict(X_test)))  # 准确率

聚类

特点

• 无监督学习：无需事先标签
• 根据相似度自动划分簇

K‑Means 示例（含参数寻优）

from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
import pandas as pd
import matplotlib.pyplot as plt

# 读取数据并进行标准化
data = pd.read_excel("air_features.xlsx", index_col="ID")
data_z = (data - data.mean()) / data.std()  # Z-score 标准化

# ========== 固定聚类数为5，进行聚类并输出中心和簇大小 ==========
kmeans_5 = KMeans(n_clusters=5, random_state=3).fit(data_z)

# 聚类中心 + 每簇数量
centers = pd.DataFrame(kmeans_5.cluster_centers_, columns=data.columns)
counts  = pd.Series(kmeans_5.labels_).value_counts().sort_index().rename("数量")
result  = pd.concat([centers, counts], axis=1)
print("K=5 聚类中心及每簇数量：")
print(result)

# ========== 对不同聚类数做指标评估，绘制Inertia和轮廓系数 ==========
sse = []
silhouette_scores = []
K_range = range(2, 11)

for k in K_range:
    kmeans = KMeans(n_clusters=k, random_state=42).fit(data_z)
    sse.append(kmeans.inertia_)
    silhouette_scores.append(silhouette_score(data_z, kmeans.labels_))

plt.figure(figsize=(10, 4))

plt.subplot(1, 2, 1)
plt.plot(K_range, sse, 'o-', color='blue')
plt.xlabel('聚类数 K')
plt.ylabel('簇内误差平方和 (Inertia)')
plt.title('Inertia - 聚类数与簇内误差平方和关系')

plt.subplot(1, 2, 2)
plt.plot(K_range, silhouette_scores, 's-', color='red')
plt.xlabel('聚类数 K')
plt.ylabel('轮廓系数')
plt.title('轮廓系数法 - 聚类数与轮廓系数关系')
plt.tight_layout()
plt.show()

关联规则

Apriori 算法

import pandas as pd
from mlxtend.preprocessing import TransactionEncoder
from mlxtend.frequent_patterns import apriori, association_rules
# 读取用户访问记录数据
info = pd.read_csv("acc_records.csv")
# 1 去重用户IP
user_ips = info["用户IP"].unique()
# 2 构建用户访问列表
url_baskets = [
 info.loc[info["用户IP"] == ip, "URL"].tolist()
 for ip in user_ips
]
# 3 One‑Hot 编码
te = TransactionEncoder()
df = pd.DataFrame(te.fit_transform(url_baskets), columns=te.columns_)
# 4 频繁项集 & 关联规则
freq_itemsets = apriori(df, min_support=0.005, use_colnames=True)
rules = association_rules(freq_itemsets, metric="confidence", min_threshold=0.05)
print(rules.sort_values("lift", ascending=False).head())